Funções de Resposta em Frequência

O comportamento dinâmico dos sistemas mecânicos é de grande importância para o projeto de produtos, verificação da integridade e segurança de equipamentos/estruturas, bem como a quantificação de riscos/falhas associadas à manutenção de componentes. Sua modelagem matemática quase sempre envolve a utilização de muitos (múltiplos) graus de liberdade tornando a análise complexa. Contudo, ao se trabalhar no regime linear, as propriedades desses sistemas complexos podem ser representadas pela soma das respostas de vários sistemas com 1 grau de liberdade (superposição modal).

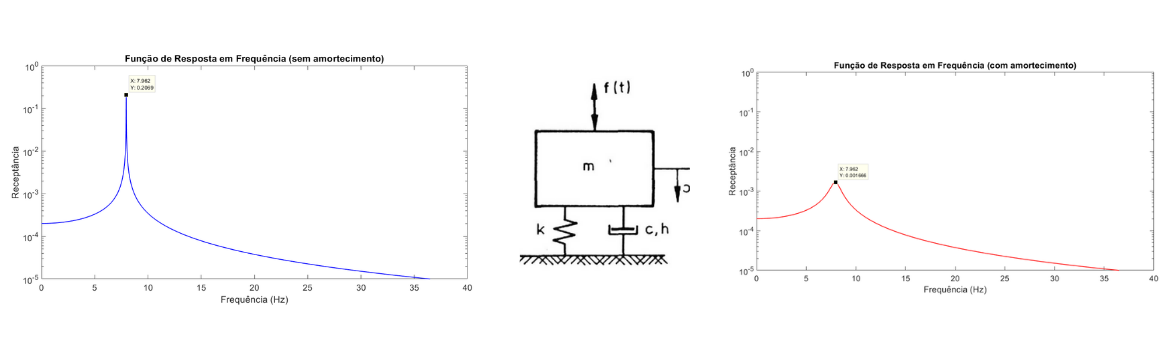
Dentre as várias análises que podem ser realizadas, a Função de Resposta em Frequência (FRF) fornece uma avaliação das propriedades estruturais como as frequências naturais, fatores de amortecimento e modos/formas de vibrar. Sendo assim, considere o sistema de um grau de liberdade abaixo:

Como já exibido nesse texto, a equação do sistema pode ser dada por:

$$ \begin{equation} m\ddot{x} + c \dot{x} + kx = f(t) \end{equation} $$

Assumindo-se um sistema sem amortecimento e com um forçamento harmônico, a resposta também será harmônica. Isso ocorre devido à natureza linear do problema. Assim, considere uma resposta e um forçamento nas formas, respectivamente: $x(t) = Xe^{i \omega t}$, $f(t) = Fe^{i \omega t}$. Realizando-se as devidas derivações e substituindo-se na equação de movimento, tem-se:

$$ \begin{equation} \frac{X}{F} = \frac{1}{k - \omega^2 m} = \alpha (\omega) \end{equation} $$

O resultado obtido é a famosa Função de Resposta em Frequência (FRF), ela fornece o comportamento do sistema em uma determinada faixa em frequência indicando onde ocorre a ressonância, efeito que deve ser evitado na maioria dos casos. Portanto, a FRF é uma excelente ferramenta que deve ser utilizada pelo engenheiro projetista de forma a garantir que o produto/projeto opere em condições seguras. A imagem abaixo exibe a FRF de um sistema com massa = 2 kg e rigidez = 5000 N/m.

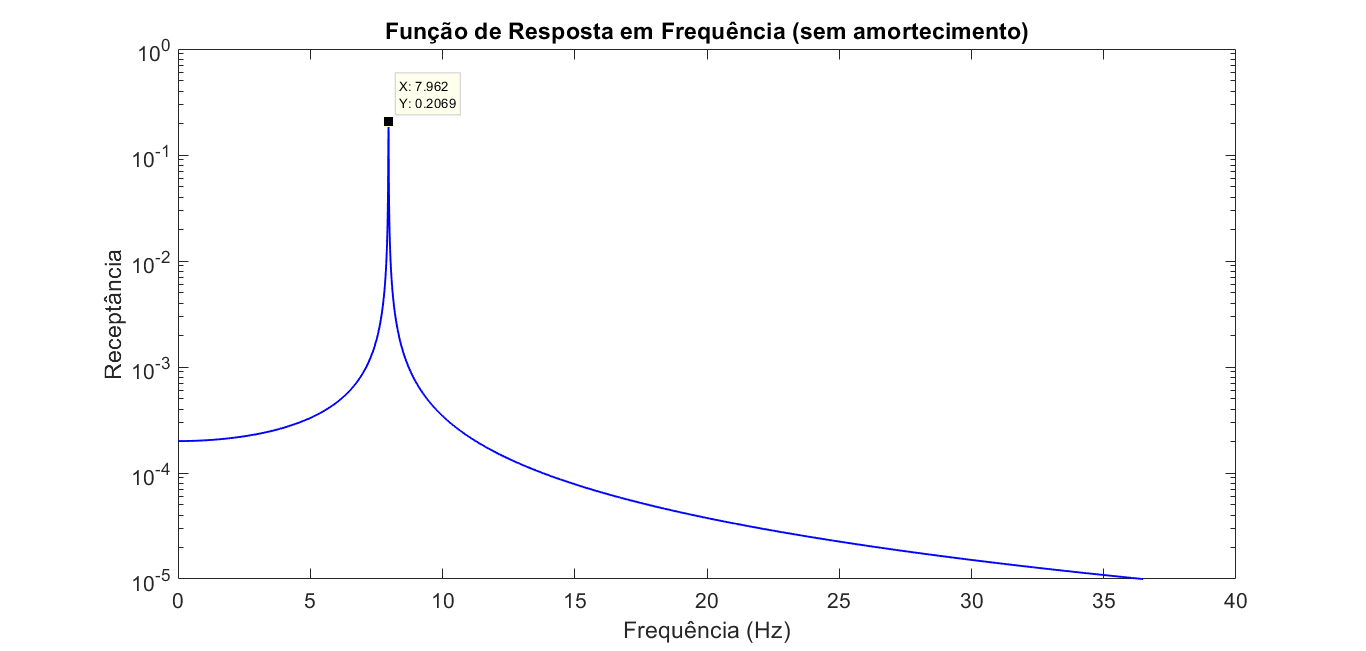
É importante notar que, devido à sua construção matemática, a FRF é independente da amplitude do forçamento, sendo esse caracterizado com amplitude unitária. Tal fato será importante ao se trabalhar com sistemas que possuem múltiplos graus de liberdade.

Ao se introduzir amortecimento no sistema, a equação passa a ter a forma: $m\ddot{x} + c \dot{x} + kx = f(t)$. Realizando-se os mesmos procedimentos para o sistema sem amortecimento, obtém-se:

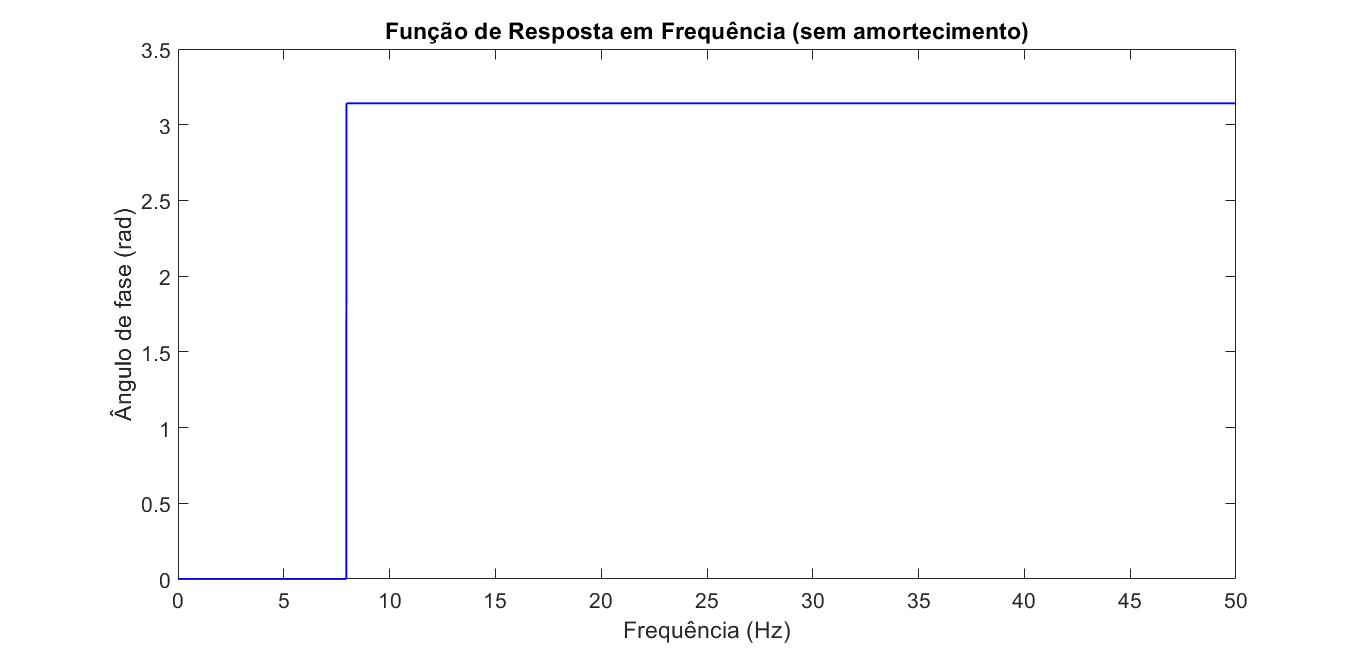
$$ \begin{equation} \frac{X}{F} = \frac{1}{k - \omega^2 m + i \omega c} = \alpha (\omega) \end{equation} $$

Observe que agora há uma parte real e outra complexa na resposta. Recordando-se dos sistemas vibratórios amortecidos, o surgimento de valores complexos indicam o comportamento de decaimento da resposta do sistema. Esses valores também são responsáveis por fornecer o ângulo de fase, sendo indispensáveis para a caracterização do comportamento total da estrutura. A imagem abaixo exibe a FRF do sistema anterior, mas com a adição de um fator de amortecimento c = 12 N.s/m. Observa-se que a introdução do amortecimento reduz a amplitude da reposta.

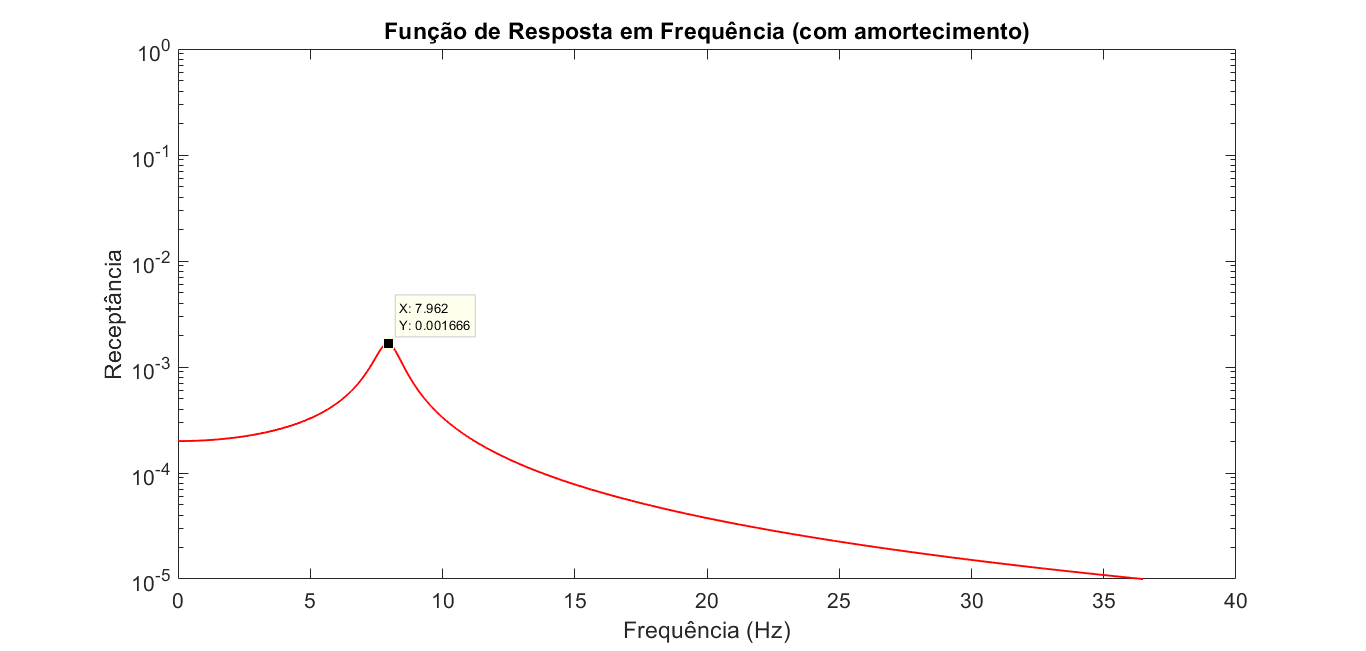
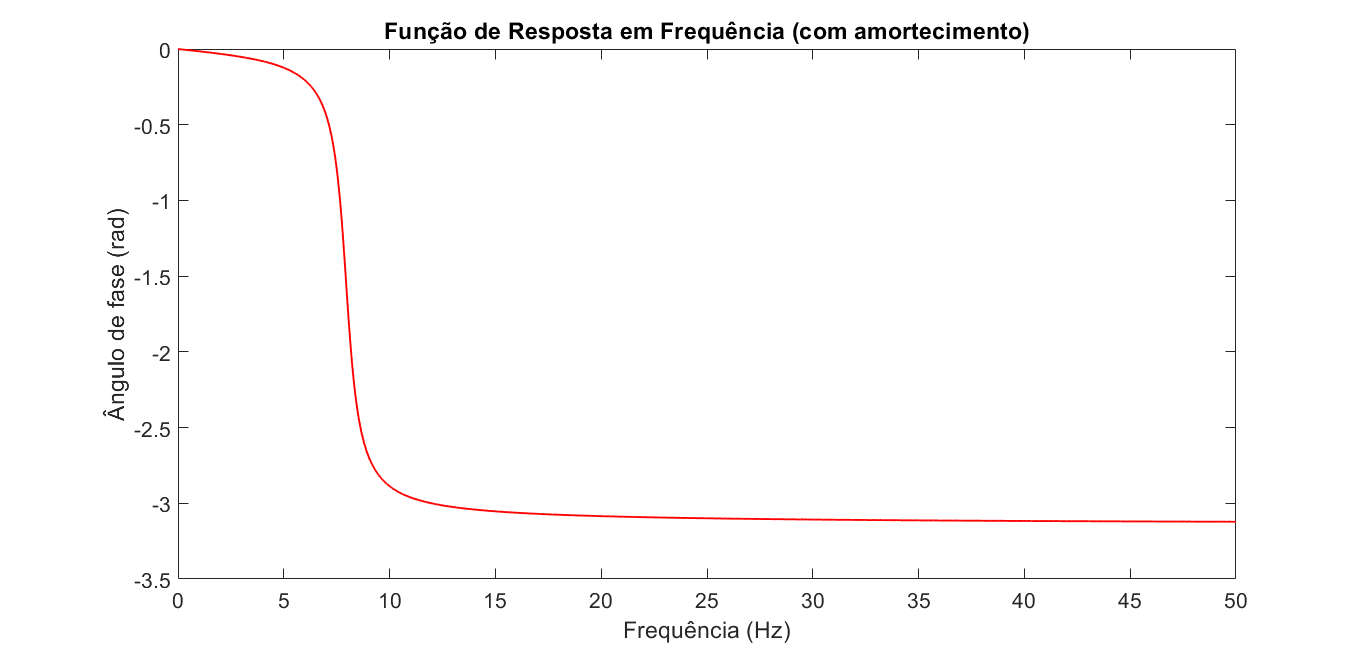
Um ponto importante é que a FRF pode ser realizada com a resposta do sistema tanto em deslocamento, como em velocidade e/ou aceleração. Isso é facilitado devido a utilização do domínio da frequência, onde as derivadas/integrais passam a ser apenas multiplicações/divisões pelos termos frequênciais. A figura abaixo exibe as principais formas das FRF's.

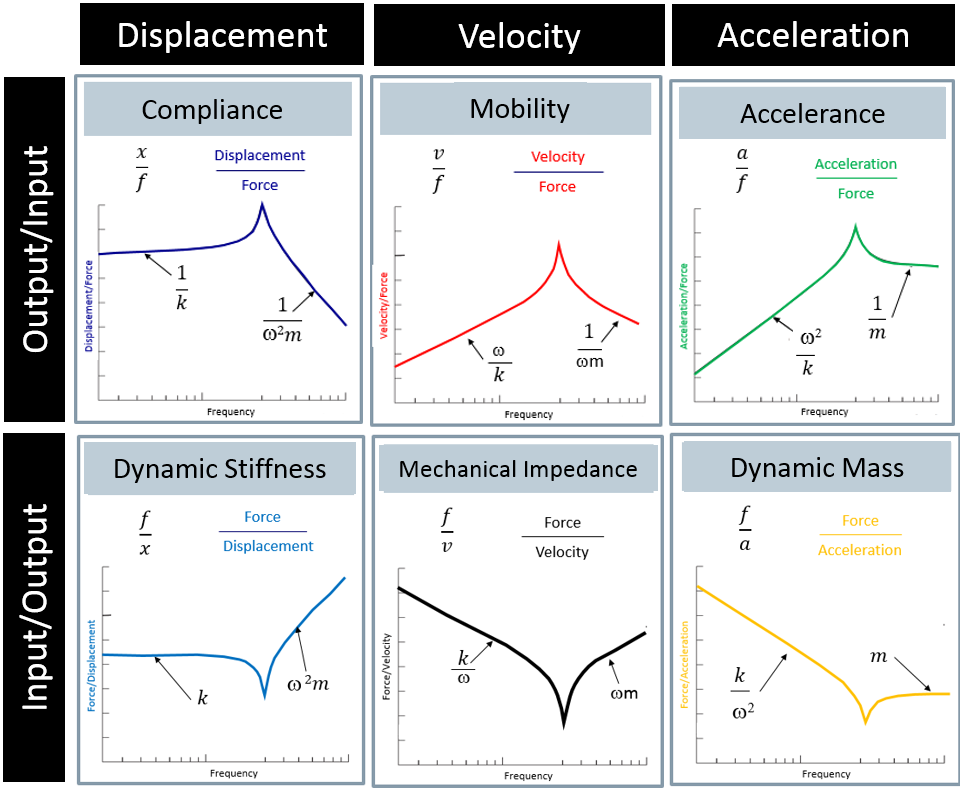
Referências:

https://community.sw.siemens.com/s/article/dynamic-stiffness-compliance-mobility-and-more

CLOUGH, R. W.; PENZIEN, J. Dynamics of structures. berkeley. CA: Computers and Structures, 2003.

DANIEL, J. I. et al. Engineering vibration. INMAN, Pearson Education, Prentice Hall,, p. 51, 2001.

JR, W. W.; TIMOSHENKO, S. P.; YOUNG, D. H. Vibration problems in engineering. [S.l.]: John Wiley &< Sons, 1990.

MEIROVITCH, L. Elements of vibration analysis. [S.l.]: McGraw-Hill Science, Engineering & Mathematics, 1975.

RAO, S. S. Vibrações mecânicas . [S.l.]: Pearson Educación, 2009.

SAVI, M. A.; PAULA, A. S. de. Vibrações mecânicas. Rio de Janeiro: LTC, p. 22, 2017.

Escrito em December 30th, 2020 por Francisco José